Le spline
di Alain Martini

«Gli sforzi degli studiosi di geometria più avanzata hanno per oggetto l'eleganza»

Evariste Galois

Perché un articolo sulle spline?

Perché ormai sono di larghissimo impiego nei settori più disparati, dal design automobilistico da cui traggono origine alle nuove frontiere dell'architettura organica passando ovviamente attraverso all'informatica.
Nel campo informatico vengono utilizzate per la grafica vettoriale, la resa dei caratteri nella tipografia digitale (ad esempio i caratteri che state leggendo ora) nonché nella realizzazione dei motori grafici 3D dei videogiochi di ultima generazione come Quake 3 Arena.

Altro fattore determinante è la semplicità, per comprenderne i meccanismi non sono necessarie grandi basi matematiche ma poche nozioni di algebra lineare e un po' di spirito di osservazione.

Eleganza ed espressività grafica.

Con la loro versatilità ed eleganza, le curve di Bézier rappresentano non solo semplici curve ma emozioni.

Prendiamo per esempio le seguenti curve:

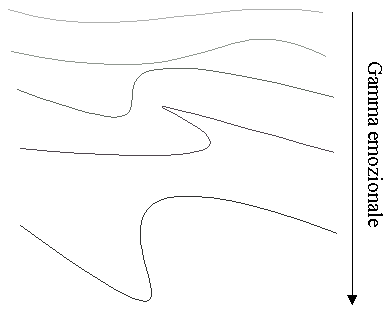
Se le esaminiamo attentamente ci rendiamo immediatamente conto del loro potere espressivo: nella figura si passa da una curva "piatta" ad una curva "tumultuosa" passando elegantemente attraverso forme prima morbide e poi taglienti.

Questo ci suggerisce che l'espressività di tali curve è legata in qualche modo alla loro curvatura. Di fatto la curvatura non è un parametro singolare di una curva, ma di tutti i punti che la costituiscono, quindi per ogni curva non avremo una singola curvatura ma un intervallo di valori di curvatura.
Tale intervallo varierà da un valore minimo ad un valore massimo, dalla una curva più "morbida" alla curva più "tagliente". L'ampiezza di tale intervallo descriverà pertanto la gamma espressiva della curva.
Prendiamo una retta o una circonferenza, queste due entità geometriche hanno in comune un intervallo di curvatura degenere, di ampiezza nulla.
La curvatura di queste infatti è sempre la stessa, zero per la retta e maggiore di zero per la circonferenza.
È per questa ragione che tratti di circonferenza o rettilinei risultano meno "emozionanti" di una curva di Bézier.

Dal punto di vista matematico possiamo inoltre osservare che la derivata prima di una curva ne descrive la velocità tangenziale, la derivata seconda è legata alla curvatura e la derivata terza indica il tasso di variazione della curvatura, pertanto più ampio è l'intervallo di curvatura più il tasso di variazione potrà avere valori elevati, "espressivi".